當前位置:日立分析儀器(上海)有限公司>>技術文章>>沒有標準樣品時如何計算測量不確定度
沒有標準樣品時如何計算測量不確定度
但當您手頭沒有標準樣品時,您該怎么做?或者是您要進行的測量不在關注區域內時又該如何處理?您可以通過應用不同的統計方法來解決這個問題。但是在我們研究這些方法之前,我們需要了解測量不確定度的相關信息。
測量不確定度的組成:正確度和精密度
正如我們在前一篇關于測量誤差的文章中所討論的那樣,準確的讀數需要滿足兩個標準:
-
平均值的準確性(正確度):這就是我們測量的平均值與預期結果的偏差。由此產生的測量誤差顯示為我們使用儀器進行每次測量時所得平均值的系統偏差。
-
精密度:如果我們多次進行相同的測量,則精密度指的是測量結果的相似度。低精密度每次都顯示出較大的波動,而高精密度得出的結果非常接近。精密度是由隨機波動造成的,因此結果遵循正態分布。
我們需要同時計算這兩個值,然后將結果組合起來,以獲得準確性的總體置信區間。
無標樣的平均值準確性計算
如果有一份已知成分的標準樣品,則只需將經認證的值與所得的平均測量值進行比較,并將結果偏移量應用于所有結果。當該方法不具有可行性時,我們必須使用另一種方法——估算標準誤差(SEE)。
下面給出了估算標準誤差的等式:
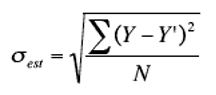
式中:
σest是估算標準誤差
Y是由儀器測定的實際結果
Y’是回歸分析后的結果
N是值的數量
使用一些實例能更容易明白該方法的原理。這是光譜儀的結果表。
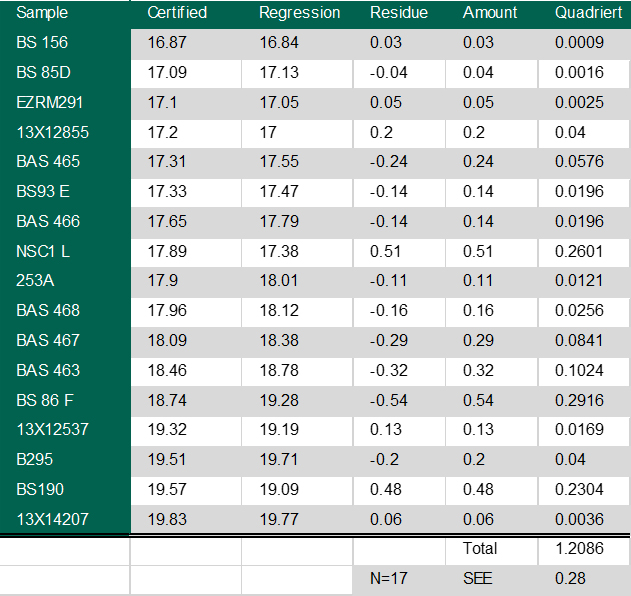
列數字是認證值,第二列是軟件應用回歸分析后的結果。在上述公式中使用這些數字得到的估算標準誤差為0.28%。
無標樣的精度計算
當由于隨機波動而不能使用GUM法測量不確定度時,我們依賴于t分布函數。這種分布函數是在樣品數量非常少的情況下開發的。
t分布函數的置信區間的表達式為:
uc= X?+/- TX?
式中:
x?:測量值的平均值
TX:t分布函數的值。根據以下公式計算:
Tx= (t (f,P) x s / N1/2
式中:
t:取自公布表格的值,該值取決于f(測量的樣品量-1)和P(期望的置信度)。
s:測量系列的標準偏差
N:采用的測量次數
假設已經測量了一個未知樣品10次,則鉻成分的測量結果如下:
10次讀數得出的平均成分:18.82%
標準偏差:0.15%。
我們將在95%的置信度內工作,需要插入上述公式的值是:
n=10
p:95%
s:0.15%
t:2.262(針對置信度為95%的P和樣品量為10)
研究這些數字會得出一個置信度。
Uc = +/-0·11%
結合正確度和精密度
現在我們已經得到了計算整體測量不確定度所需的一切要素。我們只需將+/-0.11%的精度值與+/-0.28%的平均值精度值相加,就可得到終結果:
C=18.82%+/-0.39%@95%的概率。
想了解更多?
在我們即將推出的指南《探索真實值——如何評估光譜測量的準確度并計算誤差范圍》中將詳細介紹這種方法和其他方法。該指南從闡述基本統計數據開始,使您了解通過不同的方法計算關于光譜測量的測量不確定度。您可以預先注冊獲取副本。



 17
17
